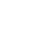线段树

什么是线段树？

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。^1

以上是百度百科给出的线段树的定义，下面我们来看一下它长啥样。

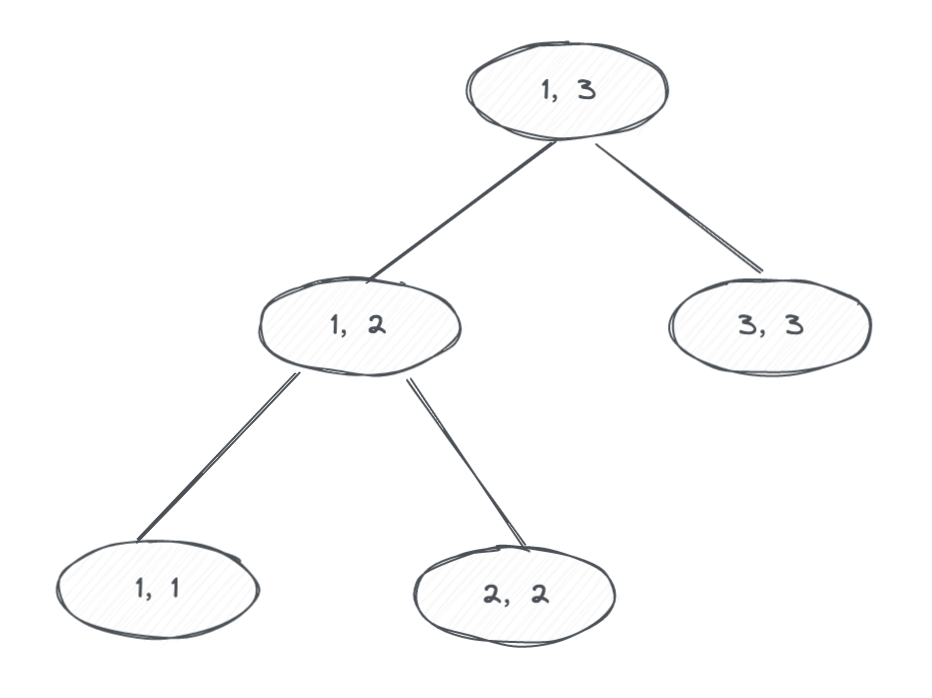
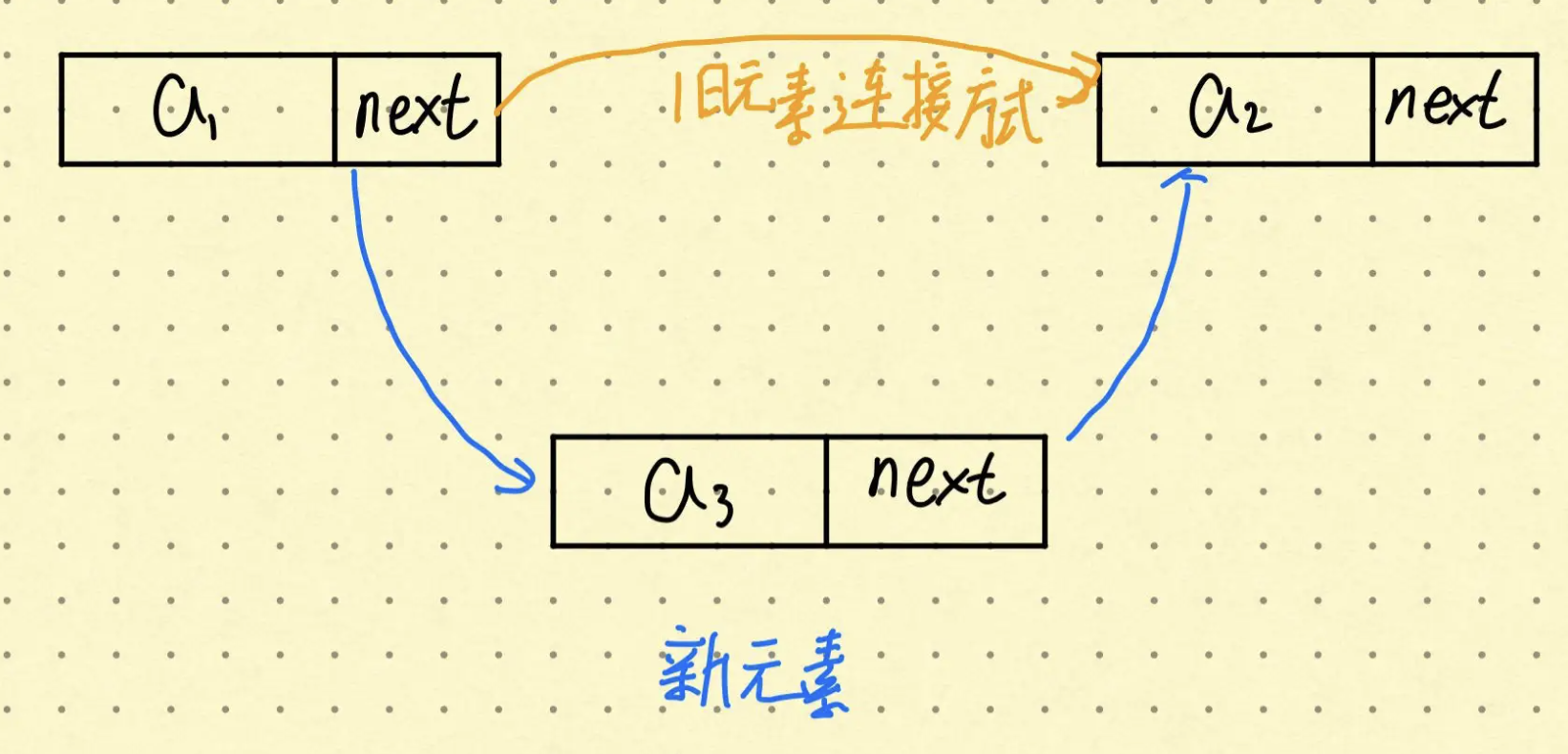
这是一个由数组[1, 2, 3]构造出来的线段树，图中每个节点代表一段区间。一般的二叉树节点上存储的是一个值，而线段树上的节点存储的是一个区间[L, R]上的聚合信息（例如最大值 / 最小值等），并且子节点的区间合并后正好等同于父节点的区间。例如，对于父节点的区间是 [L,R]，那么左子节点的区间是 [L,(L+R)/2]，右子节点的区间是 [(L+R)/2,R]。叶子节点也是一个区间，不过区间端点 L==R，是一个单点区间。

线段树能做什么？

线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。更可以扩充到二维线段树（矩阵树）和三维线段树（空间树）。对于一维线段树来说，每次更新以及查询的时间复杂度为O(logN)。

重点在于 区间操作，如果脱离了区间，线段树就没有优势了。

怎么实现线段树？

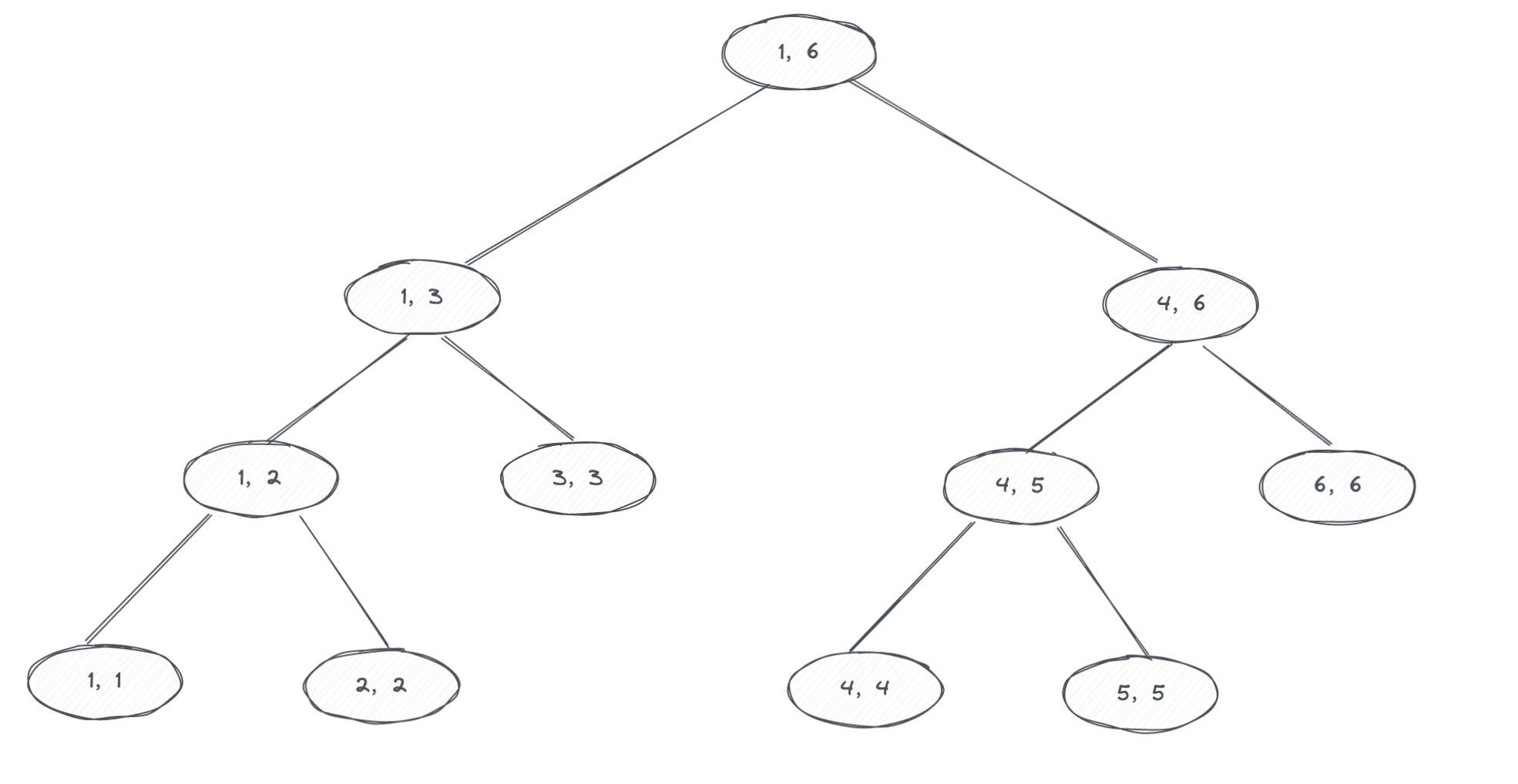
我们通常使用数组或者链表来实现线段树，因为线段树是平衡二叉树，所以使用数组操作起来更简单，空间利用率也是比较高的（除了最后一层存在空余位置之外，其它层是铺满的）。

树的根节点可以固定在 0 位置，也可以固定在 1 位置，推荐放置在 1 位置，因为在1位置下标操作不会太繁琐

根节点在 0

相对于 i 位置上的节点，其左子树在2*i+1，右子树在 2*i+2，其父节点在(i-1)/2

根节点在 1

相对于 i 位置上的节点，其左子树在2*i，右子树在 2*i+1，其父节点在i/2

构建

通过递归更新区间内的值，当区间左右两个坐标一致时说明是叶子节点，直接赋值，如果不是也叶子节点，按照需要给节点赋值，伪码如下

build(idx, left, right) {
  if(left === right) {
    segment[idx] = baseNums[left]
  }
  mid = (left + right) >> 1
  build(idx * 2, left, mid)
  build(idx * 2 + 1, mid + 1, right)
  
  // 这里是求和，可以根据要求储存最小值、最大值……
  segment[idx] = segment[idx * 2] + segment[idx * 2 + 1]
}

更新

同样的，更新操作也需要递归处理，不仅要更新叶子节点，也要更新他的所有父辈节点，伪码如下

update(target, value, idx, left, right) {
  if(left === right) {
    segment[idx] = value
  }
  
  mid = (left + right) >> 1
  if(target <= mid) {
    change(target, value,idx * 2, left, mid)
  } else {
    change(target, value, idx * 2 + 1, mid + 1, right)
  }
  // 这里是求和，可以根据要求储存最小值、最大值……
  segment[idx] = segment[idx * 2] + segment[idx * 2 + 1]
}

查询

查询操作亦是如此，因为每个结点都保留了所有子节点中的信息，所以，只要找到符合要求的区间即可。

大致有三种情况，全部在左子树、全部在右子树、左右子树各有一部分

query(start, end, idx, left, right) {
  if(start === left && end === right)
    return segment[idx]
  
  mid = (left + right) >> 1
  if(end <= mid)
    return query(start, end, idx * 2, left, mid)
  else if(start > mid)
    return query(start, end, idx * 2 + 1, mid + 1, right)
  else
    // 这里是求和，可以根据要求储存最小值、最大值……
    retuen query(start, end, idx * 2, left, mid) + 
      query(start, end, idx * 2 + 1, mid + 1, right)
}

实战演练

leetcode：307. 区域和检索 - 数组可修改

给你一个数组 nums ，请你完成两类查询。

其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right
实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值 更新 为 val
int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], …, nums[right]）

题目中已经说明了是区间操作，那么在提醒我们使用线段树来解决这个问题，当然这个问题是可以通过暴力完成的，但是，那样做题也没有什么意义了。

现看暴力的解法，很简单

class NumArray {
  private nums: number[];
  constructor(nums: number[]) {
    this.nums = nums;
  }

  update(index: number, val: number): void {
    this.nums[index] = val
  }

  sumRange(left: number, right: number): number {
    let ans = 0

    for (let i = left; i <= right; i++) {
      ans += this.nums[i]
    }

    return ans
  }
}

下面的是暴力解法，上面的是线段树，可以看出跑测试用例的时间差距还是很大的

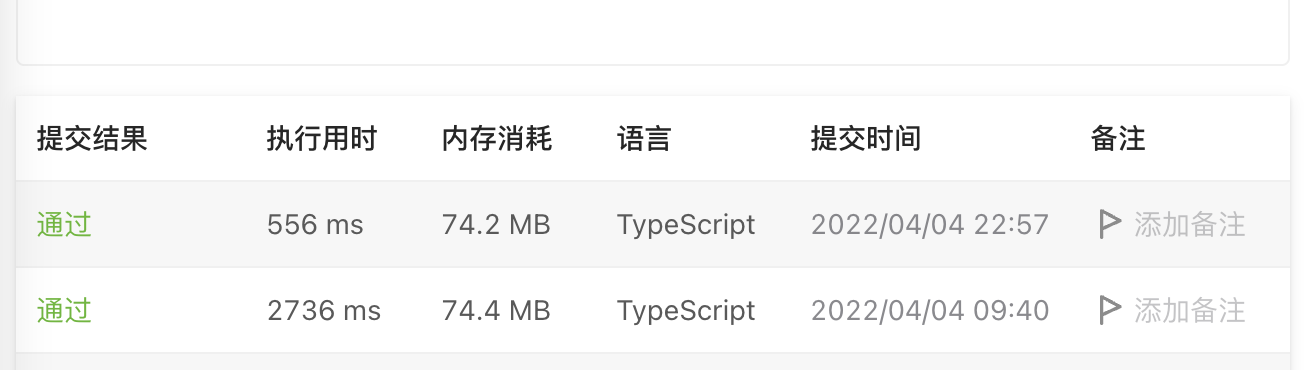
下面进入正题，来看一下线段树的解法，首先我们来定义一个 SegmentTree 构造函数，用于生成线段树

class SegmentTree {
  private segment: number[]
  private baseNums: number[];
  constructor(nums: number[]) {
    this.baseNums = nums;
    this.segment = new Array(nums.length * 4).fill(0)
    this.build(1)
  }

  build(
    idx: number,
    left: number = 0,
    right: number = this.baseNums.length - 1
  ): void {
    if (left === right) {
      // 如果是叶子节点直接赋值
      this.segment[idx] = this.baseNums[left]
      return
    }

    let mid = (left + right) >> 1
    // 分别处理左右子树
    this.build(this.leftChild(idx), left, mid)
    this.build(this.rightChild(idx), mid + 1, right)

    // 父节点存放子节点的和
    this.segment[idx] = this.segment[this.leftChild(idx)] + this.segment[this.rightChild(idx)]
  }

  change(
    target: number,
    value: number,
    idx: number = 1,
    left: number = 0,
    right: number = this.baseNums.length - 1
  ): void {
    if (left === right) {
      this.segment[idx] = value
      return
    }

    let mid = (left + right) >> 1
    if (target <= mid)
      this.change(target, value, this.leftChild(idx), left, mid)
    else
      this.change(target, value, this.rightChild(idx), mid + 1, right)

    this.segment[idx] = this.segment[this.leftChild(idx)] + this.segment[this.rightChild(idx)]
  }

  range(
    start: number,
    end: number,
    idx: number = 1,
    left: number = 0,
    right: number = this.baseNums.length - 1
  ): number {
    if (left === start && right === end) {
      return this.segment[idx]
    }

    let mid = (left + right) >> 1

    if (end <= mid)
      return this.range(start, end, this.leftChild(idx), mid + 1, right)
    else if (start > mid)
      return this.range(start, end, this.rightChild(idx), left, mid)
    else
      return this.range(start, end, this.leftChild(idx), mid + 1, right) +
        this.range(start, end, this.rightChild(idx), left, mid)
  }

  leftChild(idx: number): number {
    return idx * 2
  }
  rightChild(idx: number): number {
    return idx * 2 + 1
  }
}

可能会有疑问为什么要初始化 4n 个空间，不是最多只有 2n-1 个节点吗？

我刚开始看的时候也有这个疑问。因为树并不是顺着排下来的，中间是有闲置空间的，如果二叉树全部排满那么 2n 空间就够用。先看一下这张图

如果层数深一点，就可能最后一层只有两组叶子节点，并且相隔很远，倒数第二层的个数约等于 n，由树的特性可以知道，最后一层大约有 2n 个结点，上层的结点约为 n -1，所以开辟 4n 的空间完全够用

回到问题，我们需要对线段树做一层包装

class NumArray1 {
  private segmentTree: SegmentTree;
  constructor(nums: number[]) {
    this.segmentTree = new SegmentTree(nums)
    this.segmentTree.build(1)
  }
  
  change(idx: number, value: number): void {
    this.segmentTree.change(idx, value)
  }

  sumRange(left: number, right: number): number {
    return this.segmentTree.range(left, right)
  }
}

来测试一下

const numArr = new NumArray1([1, 3, 5])

console.log(numArr.sumRange(0, 2)); // 9
numArr.change(1, 2)
console.log(numArr.sumRange(0, 2)); // 8