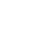最近业务上碰到了浮点数计算的相关问题，特此调研记录

image-20230704115709074

浮点数计算精度丢失的原因

同其他大部分的编程语言一样，JavaScript 的浮点数采用了 IEEE754 双精度浮点数标准（事实上整数也采用此标准），先来简单复习下 IEEE754 标准的具体内容。

单精度浮点数（32位）：

  • 符号位（1位）：用于表示正数或负数。0 表示正数，1 表示负数。

  • 指数位（8位）：用于表示指数的偏移量。通过对指数进行偏移，可以表示非常大或非常小的数值范围。

  • 尾数位（23位）：用于表示有效数字的尾数部分。

双精度浮点数（64位）：

  • 符号位（1位）：同样用于表示正数或负数。

  • 指数位（11位）：比单精度浮点数多出的位数用于更广范围的指数偏移。

  • 尾数位（52位）：比单精度浮点数多出的位数用于更高的精度。

以10.625双精度浮点数为例，其存储方式如下图

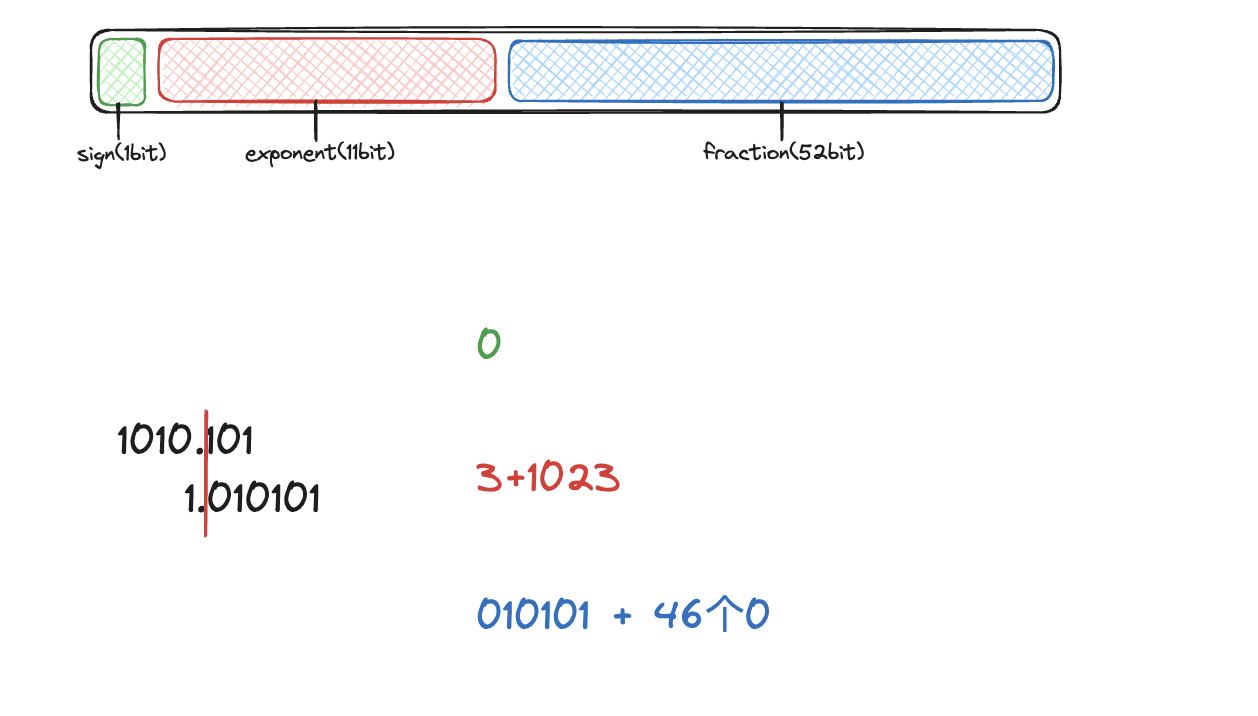
image-20230702203731746

借助二进制计算工具binaryconvert可以看到它的二进制形式

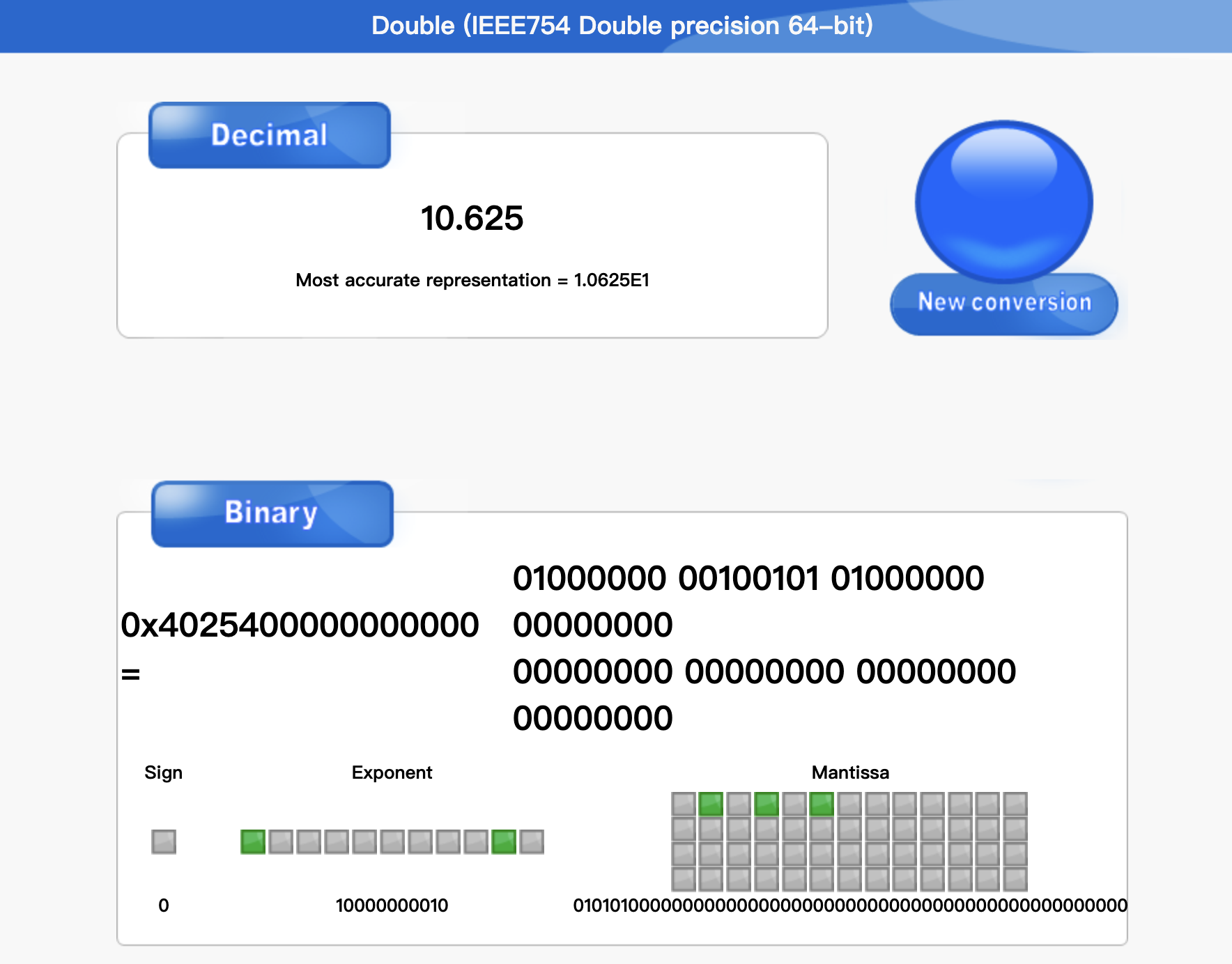
image-20230704082655039

双精度浮点数二进制计算方式：

  1. 符号位根据正负号确定；
  2. 整数位和小数位分别计算二进制，整数部分和整形二进制计算一致，小数部分二进制计算方式为乘二取整，例如0.625 * 2 = 1.250那么第一位便为1，然后用小数部分0.25继续乘下去 0.25 * 2 = 0.5 第二位便为0，再重复一次之后取整数1小数位为0停止计算，剩余bit补0，如果小数位不为零则继续计算下去直到52位全部填满；
  3. 计算指数位，将整数位进行移动，保持整数位是1，小数点左移为正右移为负，然后添加偏移量1023，转为二进制便为指数位(移动时继续截断)；
  4. 此时小数点后的部分便为最终尾数位。

到这里关于为什么存在精度丢失问题已经有结论了，因为尾数位最大只有52位，有些数计算二进制是无限循环的，超出之后被截断就会造成精度丢失

常见的解决浮点数计算的方案

先转为整数再进行计算

例如在计算1.1 - 0.002时，先找出两个小数转为整数时需要乘的10^n（即小数点移动的位数），然后进行运算，最后将结果进行还原之后返回。

例如

// 计算尾数部分的长度
function getFractionalPartLength(floatString: string) {
    return (floatString.split('.')[1] || '').length;
}

// 浮点数转整形
function float2Int(float: string, base: number) {
    return Math.round(Number(float) * base);
    // 或者
    // const fraction = float.split('.')[1] || '';
    // if (fraction.length > base) {
    //     throw new Error('无法转为整数')
    // }
    // if (fraction.length < base) {
    //     float.concat(
    //         Array.from({length: base - fraction.length})
    //         .fill('0')
    //         .join('')
    //     )
    // }
    
    // return Number(float.split('.').join(''))
}

function floatSubtractCompute(minuend: string, subtrahend: string) {
    // 计算将两个浮点转为整数的最小基数
    const max = Math.max(getFractionalPart(minuend), getFractionalPart(subtrahend));
    const base = Math.pow(10, max);
    // 转为整数并计算差值
    const result = float2Int(minuend, base) - float2Int(subtrahend, base);
    return result / base;
}

big.js

big.js 是一个面向对象的用于解决 JavaScript 中运算丢失精度的第三方库，凭借其优秀表现已经在 GitHub 获得了 4.4k Star，可以借用它来解决浮点数运算精度丢失问题。

const num = new Big(0.1);
num.add(0.2).toString(); // '0.3'
num.sub(0.1).toString(); // '0.1'
0.1 + 0.2 // 0.30000000000000004

其主要的运算方法可以进行链式调用

const a = new Big(100);
a.add(30).sub(10).div(2).mul(3).toString(); // 180

因为其计算结果是Big实例，所以在显示时需要手动调用toString()转为字符串进行显示。

TS类型声明需要从@types/big.js获得

big.js 的源码并不适合阅读，尤其在变量命名方面，使用了大量的单个字母的组合阅读起来比较困难。

可以通过实例简单分析一下big.js的原理

image-20230704185552518

在Big构造函数中，通过parse函数将传入的number进行格式化，将每一个数位进行拆分，作为数组保存在c属性中，小数点所在的位置保存为e属性，正负号保存为s属性。

number-precision

number-precision 是一个函数式的运算库，在 GitHub 也有着 3.8k Star 的优秀表现。

NP.plus(num1, num2, num3, ...)   // 加
NP.minus(num1, num2, num3, ...)  // 减
NP.times(num1, num2, num3, ...)  // 乘
NP.divide(num1, num2, num3, ...) // 除
NP.round(num, ratio)  // 根据比例舍入

其底层实现也是利用上上面说的转整数计算再还原的方法。

还有一种对于前端来说最简单的办法——让后端计算。

赏

前端小白